Trojuholníky napätí, odporov a výkonov

Každý, kto má predstavu o vektorových diagramoch, si ľahko všimne, že na nich možno veľmi jasne rozlíšiť pravouhlý trojuholník napätia, ktorého každá strana odráža: celkové napätie obvodu, napätie aktívneho odporu a napätie na reaktancii.

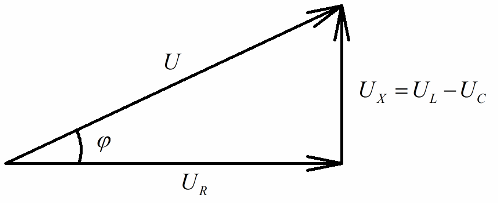
V súlade s Pytagorovou vetou bude vzťah medzi týmito napätiami (medzi celkovým napätím obvodu a napätím jeho častí) vyzerať takto:

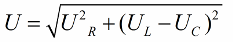
Ak je ďalším krokom rozdelenie hodnôt týchto napätí prúdom (prúd preteká všetkými časťami sériového obvodu rovnako), potom Ohmov zákon dostaneme hodnoty odporu, to znamená, že teraz môžeme hovoriť o pravouhlom trojuholníku odporov:

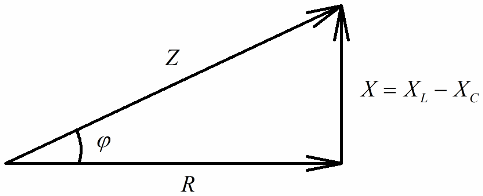
Podobným spôsobom (ako v prípade napätí), pomocou Pytagorovej vety, je možné stanoviť vzťah medzi impedanciou obvodu a reaktanciami. Vzťah bude vyjadrený nasledujúcim vzorcom:

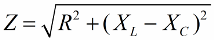
Potom vynásobíme hodnoty odporu prúdom, v skutočnosti zvýšime každú stranu pravouhlého trojuholníka o určitý počet krát. Výsledkom je pravouhlý trojuholník s kapacitami:

Aktívny výkon uvoľnený pri aktívnom odpore obvodu spojený s nevratnou premenou elektrickej energie (na teplo, pri výkone práce v inštalácii) bude jednoznačne súvisieť s jalovým výkonom zapojeným do reverzibilnej premeny energie (vytvorenie magnetického a elektrického poľa v cievkach a kondenzátoroch) a s plným výkonom dodávaným do elektrickej inštalácie.

Aktívny výkon sa meria vo wattoch (W), jalový výkon — vo varis (VAR — voltampérový reaktívny), celkový — vo VA (voltampér).

Podľa Pytagorovej vety máme právo písať:

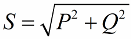
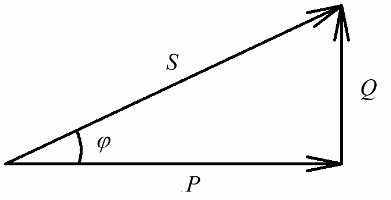
Venujme teraz pozornosť tomu, že vo výkonovom trojuholníku je uhol fí, ktorého kosínus sa dá ľahko určiť predovšetkým podľa činného výkonu a zdanlivého výkonu. Kosínus tohto uhla (cos phi) nazývaný účinník. Ukazuje, koľko z celkového výkonu pripadá na užitočnú prácu v elektroinštalácii a nevracia sa do siete.

Je zrejmé, že vyšší účinník (maximálny jeden) naznačuje vyššiu účinnosť premeny energie dodanej do zariadenia na prevádzku. Ak je účinník 1, potom sa všetka dodaná energia spotrebuje na prácu.

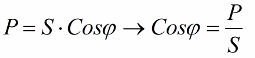
Získané pomery umožňujú vyjadrenie aktuálnej spotreby inštalácie z hľadiska účinníka, činného výkonu a sieťového napätia:

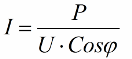
Takže čím je kosínus phi menší, tým väčší prúd potrebuje sieť na vykonanie určitej úlohy. V praxi tento faktor (maximálny sieťový prúd) obmedzuje prenosovú kapacitu prenosovej linky, a preto čím nižší je účinník, tým väčšie je zaťaženie linky a tým nižšia je užitočná šírka pásma (nízky kosínus phi vedie k obmedzeniu ). Straty joulov v elektrických vedeniach s klesajúcim kosínusovým phi možno vidieť z nasledujúceho vzorca:

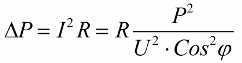
Na aktívnom odpore R prenosového vedenia sa straty zvyšujú tým viac, čím je vyšší prúd I, aj keď je reaktívny na záťaž. Preto môžeme povedať, že pri nízkom účinníku sa náklady na prenos elektriny jednoducho zvyšujú. To znamená, že zvyšovanie kosínusového phi je dôležitou národnou ekonomickou úlohou.

Je žiadúce, aby sa jalová zložka celkového výkonu blížila k nule.K tomu by bolo dobré používať elektromotory a transformátory vždy pri plnom zaťažení a po skončení používania ich vypnúť, aby nestáli naprázdno. Pri voľnobehu majú motory a transformátory veľmi nízky účinník. Jedným zo spôsobov, ako zvýšiť kosínusové phi u používateľov, je použitie kondenzátorové banky a synchrónne kompenzátory.