Elektrón v elektrickom poli

Pohyb elektrónu v elektrickom poli je jedným z najdôležitejších fyzikálnych procesov pre elektrotechniku. obrázok Pozrime sa, ako sa to deje vo vákuu. Uvažujme najprv o príklade pohybu elektrónu z katódy na anódu v rovnomernom elektrickom poli.

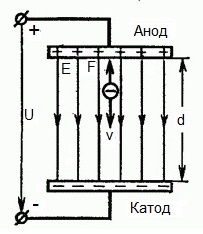
Obrázok nižšie ukazuje situáciu, kedy elektrón opúšťa zápornú elektródu (katódu) so zanedbateľne malou počiatočnou rýchlosťou (s tendenciou k nule) a vstupuje v rovnomernom elektrickom poliprítomný medzi dvoma elektródami.

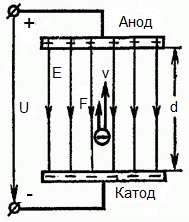
Na elektródy sa aplikuje konštantné napätie U a elektrické pole má zodpovedajúcu silu E. Vzdialenosť medzi elektródami sa rovná d. V tomto prípade bude na elektrón pôsobiť sila F zo strany poľa, ktorá je úmerná náboju elektrónu a sile poľa:

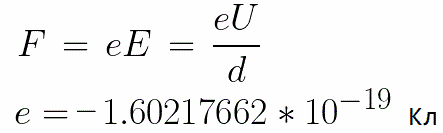
Pretože elektrón má záporný náboj, táto sila bude nasmerovaná proti vektoru intenzity poľa E. V súlade s tým bude elektrón v tomto smere urýchľovaný elektrickým poľom.

Zrýchlenie elektrónu je úmerné veľkosti sily F, ktorá naň pôsobí, a nepriamo úmerné hmotnosti elektrónu m.Keďže pole je rovnomerné, zrýchlenie pre daný obrázok možno vyjadriť ako:

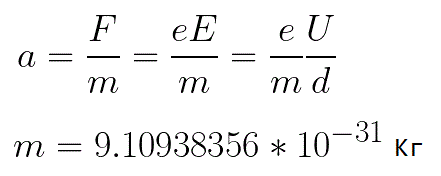
V tomto vzorci je pomer náboja elektrónu k jeho hmotnosti špecifický náboj elektrónu, množstvo, ktoré je fyzikálnou konštantou:

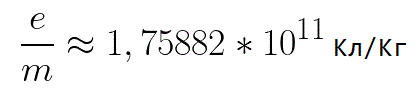
Elektrón je teda v zrýchľujúcom sa elektrickom poli, pretože smer počiatočnej rýchlosti v0 sa zhoduje so smerom sily F na strane poľa a preto sa elektrón pohybuje rovnomerne. Ak nie sú žiadne prekážky, prejde dráhu d medzi elektródami a dosiahne anódu (kladnú elektródu) s určitou rýchlosťou v. V okamihu, keď elektrón dosiahne anódu, jeho kinetická energia sa bude zodpovedajúcim spôsobom rovnať:

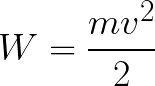
Keďže po celej dráhe d je elektrón urýchľovaný silami elektrického poľa, získava túto kinetickú energiu ako výsledok práce sily pôsobiacej na stranu poľa. Táto práca sa rovná:

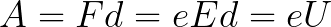
Potom kinetickú energiu získanú elektrónom pohybujúcim sa v poli možno nájsť takto:

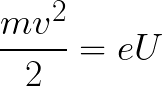
To znamená, že to nie je nič iné ako práca síl poľa na urýchlenie elektrónu medzi bodmi s potenciálnym rozdielom U.

V takýchto situáciách je na vyjadrenie energie elektrónu vhodné použiť takú jednotku merania ako "elektrónvolt", ktorá sa rovná energii elektrónu pri napätí 1 volt. A keďže elektrónový náboj je konštantný, potom 1 elektrovolt je tiež konštantná hodnota:

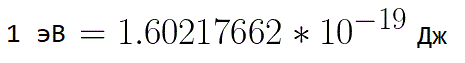
Z predchádzajúceho vzorca môžete ľahko určiť rýchlosť elektrónu v ktoromkoľvek bode jeho dráhy pri pohybe v zrýchľujúcom sa elektrickom poli, pričom poznáte iba potenciálny rozdiel, ktorý prešiel pri zrýchlení:

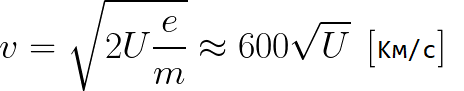
Ako vidíme, rýchlosť elektrónu v urýchľujúcom poli závisí iba od rozdielu potenciálu U medzi koncovým bodom a počiatočným bodom jeho dráhy.

Predstavte si, že elektrón sa začne pohybovať od katódy zanedbateľnou rýchlosťou a napätie medzi katódou a anódou je 400 voltov. V tomto prípade bude v okamihu dosiahnutia anódy jej rýchlosť rovná:

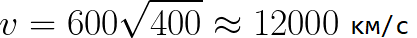
Je tiež ľahké určiť čas potrebný na to, aby elektrón prekonal vzdialenosť d medzi elektródami. Pri rovnomerne zrýchlenom pohybe z pokoja sa zistí, že priemerná rýchlosť je polovica konečnej rýchlosti, potom sa čas zrýchleného letu v elektrickom poli bude rovnať:

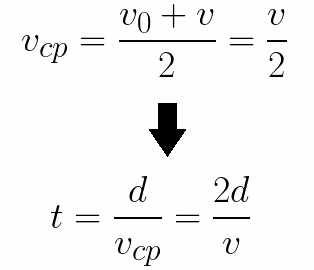
Uvažujme teraz o príklade, keď sa elektrón pohybuje v spomaľujúcom sa rovnomernom elektrickom poli, to znamená, že pole smeruje ako predtým, ale elektrón sa začína pohybovať opačným smerom - od anódy ku katóde.

Predpokladajme, že elektrón opustil anódu s určitou počiatočnou rýchlosťou v a spočiatku sa začal pohybovať v smere katódy. V tomto prípade bude sila F pôsobiaca na elektrón zo strany elektrického poľa smerovať proti vektoru elektrickej intenzity E — od katódy k anóde.

Začne znižovať počiatočnú rýchlosť elektrónu, to znamená, že pole spomalí elektrón. To znamená, že elektrón sa za týchto podmienok začne pohybovať rovnomerne a rovnomerne pomaly. Situácia je opísaná takto: "elektrón sa pohybuje v spomaľujúcom elektrickom poli."

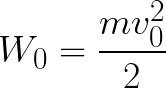
Od anódy sa elektrón začal pohybovať s nenulovou kinetickou energiou, ktorá sa pri spomaľovaní začína znižovať, keďže energia sa teraz vynakladá na prekonávanie sily pôsobiacej z poľa na elektrón.

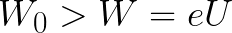
Ak by počiatočná kinetická energia elektrónu pri výstupe z anódy bola okamžite väčšia ako energia, ktorú musí pole vynaložiť na urýchlenie pohybu elektrónu z katódy na anódu (ako v prvom príklade), potom by elektrón prejsť vzdialenosť d a nakoniec dosiahne katódu napriek brzdeniu.

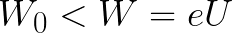
Ak je počiatočná kinetická energia elektrónu menšia ako táto kritická hodnota, potom elektrón nedosiahne katódu. V určitom bode sa zastaví a potom začne rovnomerne zrýchlený pohyb späť k anóde. Výsledkom je, že pole mu vráti energiu, ktorá bola vynaložená na proces zastavenia.

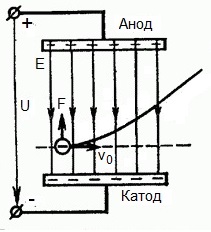
Ale čo ak elektrón letí rýchlosťou v0 v oblasti pôsobenia elektrického poľa v pravom uhle? Je zrejmé, že sila na strane poľa v tejto oblasti smeruje pre elektrón od katódy k anóde, to znamená proti vektoru intenzity elektrického poľa E.

To znamená, že teraz má elektrón dve zložky pohybu: prvá - s rýchlosťou v0 kolmá na pole, druhá - rovnomerne zrýchlená pôsobením sily zo strany poľa smerujúcej k anóde.

Ukazuje sa, že po lete do poľa pôsobenia sa elektrón pohybuje po parabolickej trajektórii. Ale po vyletení z oblasti pôsobenia poľa bude elektrón pokračovať vo svojom rovnomernom pohybe zotrvačnosťou po priamke.