Topológie obvodov – základné pojmy

Elektrický obvod je súbor zariadení (prvkov) a ich spojovacích vodičov, ktorými môže pretekať elektrický prúd. Všetky prvky elektrických obvodov zdieľajú v pasívnom a aktívnom.

Aktívne prvky premieňajú rôzne druhy energie (mechanickú, chemickú, svetelnú atď.) na elektrickú energiu. V pasívnych zariadeniach sa elektrická energia premieňa na iné druhy energie. Aktívne prvky sa nazývajú zdroje, pasívne spotrebitelia alebo prijímače.

V teórii obvodov sa berú do úvahy idealizované modely elektrických prvkov. Vďaka tomu je popis prvkov čo najjednoduchší. Zložitejšie, reálne prvky sú modelované zo súboru idealizovaných prvkov.

Hlavnými pasívnymi prvkami elektrických obvodov sú rezistor (odporový prvok), induktor (indukčný prvok) a kondenzátor (kapacitný prvok). Prvky sú inštalované v elektrickom obvode na generovanie napätia a prúdu danej hodnoty a tvaru (pozri — Elektrický obvod a jeho prvky).

Elektrický obvod pozostáva z vetiev a uzlov. Pobočka — toto je časť elektrického obvodu (obvodu), cez ktorý preteká rovnaký prúd. Uzol — spojenie troch alebo viacerých vetiev. Na elektrickej schéme je uzol označený bodkou (obr. 1).

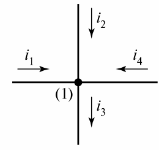
Ryža. 1. Definujte uzol v diagrame

V prípade potreby sú uzly diagramu očíslované zľava doprava zhora nadol.

Na obr. 2 je znázornená odporovo-kapacitná vetva, v ktorej tečie prúd iC.

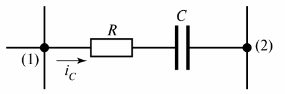
Ryža. 2. Odporovo-kapacitná vetva

Môže byť uvedená iná definícia vetvy — je to úsek obvodu medzi dvoma susednými uzlami (uzly (1) a (2) na obr. 2).

reťaz Existuje nejaká uzavretá cesta v elektrickom obvode. Obvod môže byť uzavretý ľubovoľnými vetvami, vrátane podmienených vetiev, ktorých odpor sa rovná nekonečnu.

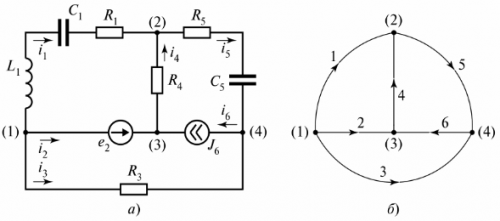
Na obr. 3 znázorňuje rozvetvený elektrický obvod, ktorý pozostáva z troch vetiev.

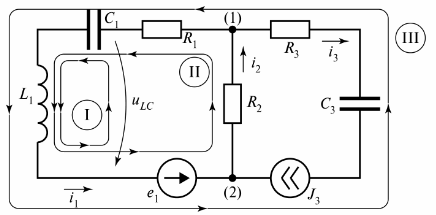
Ryža. 3. Elektrický obvod s dvoma obvodmi

Diagram ukazuje tri okruhy a okruh I je uzavretý vetvou nekonečného odporu. Táto vetva je označená ako napätie tiLC.

Pre obvod z obr. 3 je možné zostaviť veľa slučiek, ktoré sú uzavreté skutočnými alebo podmienenými vetvami, ale na výpočet elektrického šumu sa používa koncept «nezávislej slučky». Počet nezávislých obvodových slučiek je vždy nastavený ako minimum potrebné pre výpočet.

Nezávislé obvody sú vždy uzavreté, ale vetvy, ktoré majú odpor nerovnajúci sa nekonečnu, a každý nezávislý obvod obsahuje aspoň jednu vetvu, ktorá nie je zahrnutá v iných obvodoch. Pre zložité elektrické obvody môžete určiť počet nezávislých obvodov pomocou schémy zapojenia.

Na schéme zapojenia nazýva sa podmienená reprezentácia obvodu, v ktorej je každá vetva nahradená úsečkou. Položky v pobočkách sa nezobrazujú. Napríklad na obr. 4 znázorňuje odbočný obvod a jeho schému.

Ryža. 4. Rozvetvený elektrický obvod: a — schéma zapojenia, b — schéma

Ak chcete vytvoriť diagram diagramu, musíte spojiť uzly s odbočkami bez toho, aby ste na nich špecifikovali prvky. Vetvy sú očíslované a smery prúdov na nich sú označené šípkami. Samotný graf nemá žiadny fyzikálny význam, ale dá sa použiť na určenie počtu a typu nezávislých obrysov. Na tento účel je pripravený „grafický strom“.

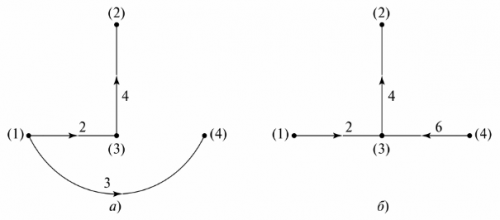
Grafický strom Predstavuje graf obvodu, ktorého uzly sú spojené vetvami takým spôsobom, že nevznikne uzavretá slučka. Na zobrazenie grafického stromu môže byť niekoľko možností. Na obr. 5 sú znázornené dve možné varianty pre obvod z obr. 4.

Ryža. 5. Grafický strom schémy

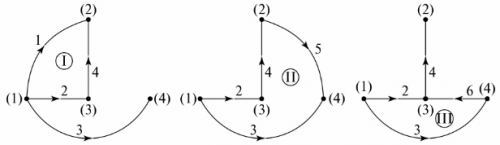
Počet chýbajúcich vetiev v strome grafu sa rovná počtu nezávislých slučiek obvodu. V príklade sú to tri vetvy, tri nezávislé slučky. Konfiguráciu nezávislých slučiek je možné získať postupným spájaním uzlov stromu grafu s vetvami, ktoré nie sú špecifikované v strome grafu. Napríklad pre strom grafov na obr. 5 a nezávislé obrysy sú znázornené na obr. 6.

Ryža. 6. Určenie nezávislých obrysov cez strom grafov

Výber možnosti konfigurácie nezávislých obvodov na výpočet obvodu sa vykonáva počas analýzy obvodu. Mali by ste zvoliť také obrysy, aby bol výpočet čo najjednoduchší, t.j. počet závislých rovníc v systéme je minimálny.

Topologické rovnice vytvárajú vzťah medzi napätiami a prúdmi v obvode a počet a typ rovníc nezávisí od toho, ktoré prvky sú zahrnuté vo vetvách. Topologické rovnice zahŕňajú rovnice zložené z podľa Kirchhoffových zákonov.